如何实现点选物体
上一节,我们了解了在 Fabric.js 中,可以通过 transform 进行矩阵运算,从而达到平移、旋转、缩放的目的。
接下来我们将了解如何对一个物体进行点选,在 Fabric.js 的表现即鼠标移动到元素上,呈现hover状态,移出则显示默认状态。

判断是否在矩形内部
如果对于矩形元素来说, 我们可以获取到四个顶点的坐标,进而判断当前的鼠标坐标是否在顶点坐标之内即可。
例如矩形的左上角顶点坐标是 left、top
那么我们只需要判断 left <= x <= left + width && top <= y <= top + height 即可。
基于此,在 Fabric.js 静态层 Canvas 会有一个 _objects 数组,存储了所有图形的数据,
此时可以通过从后往前遍历(因为最后添加元素位于数组最后)判断鼠标点是否在元素上。
包围盒
对于其他图形,例如三角形等,可以引入包围盒的概念,将其他图形转化为矩形进行判断。
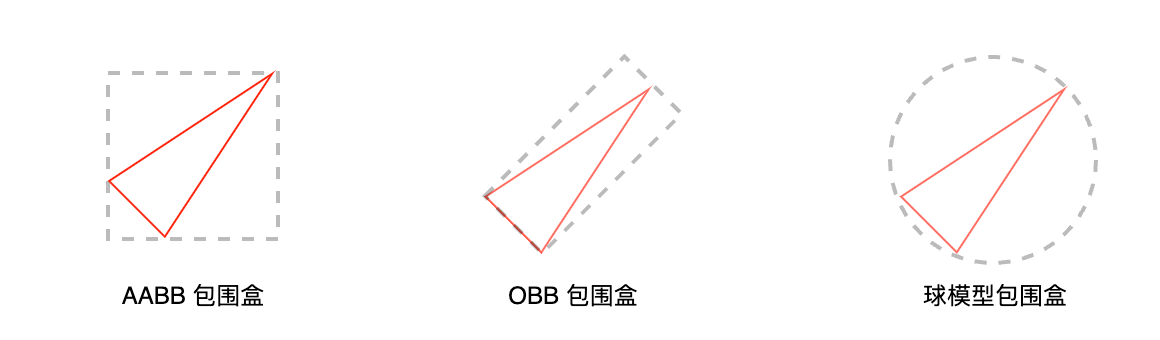
常见的有 OBB、AABB、球模型包围盒
| 类型 | 特点 | 优点 | 缺点 | 应用场景 |
|---|---|---|---|---|
| AABB(轴对齐包围盒) | 边与坐标轴对齐,由最小点和最大点定义 | 计算简单,存储效率高 | 对旋转物体可能不紧凑,浪费空间 | 静态场景筛选,粗略碰撞检测 |
| OBB(方向包围盒) | 可任意旋转,由中心点、尺寸向量和旋转矩阵描述 | 更紧凑地包围旋转物体 | 计算复杂度高 | 精确碰撞检测,动态物体包围 |
| 球模型包围盒 | 以中心点和半径定义 | 旋转无影响,检测简单 | 对非球状物体浪费较多空间 | 初步碰撞检测,三维场景快速筛选 |
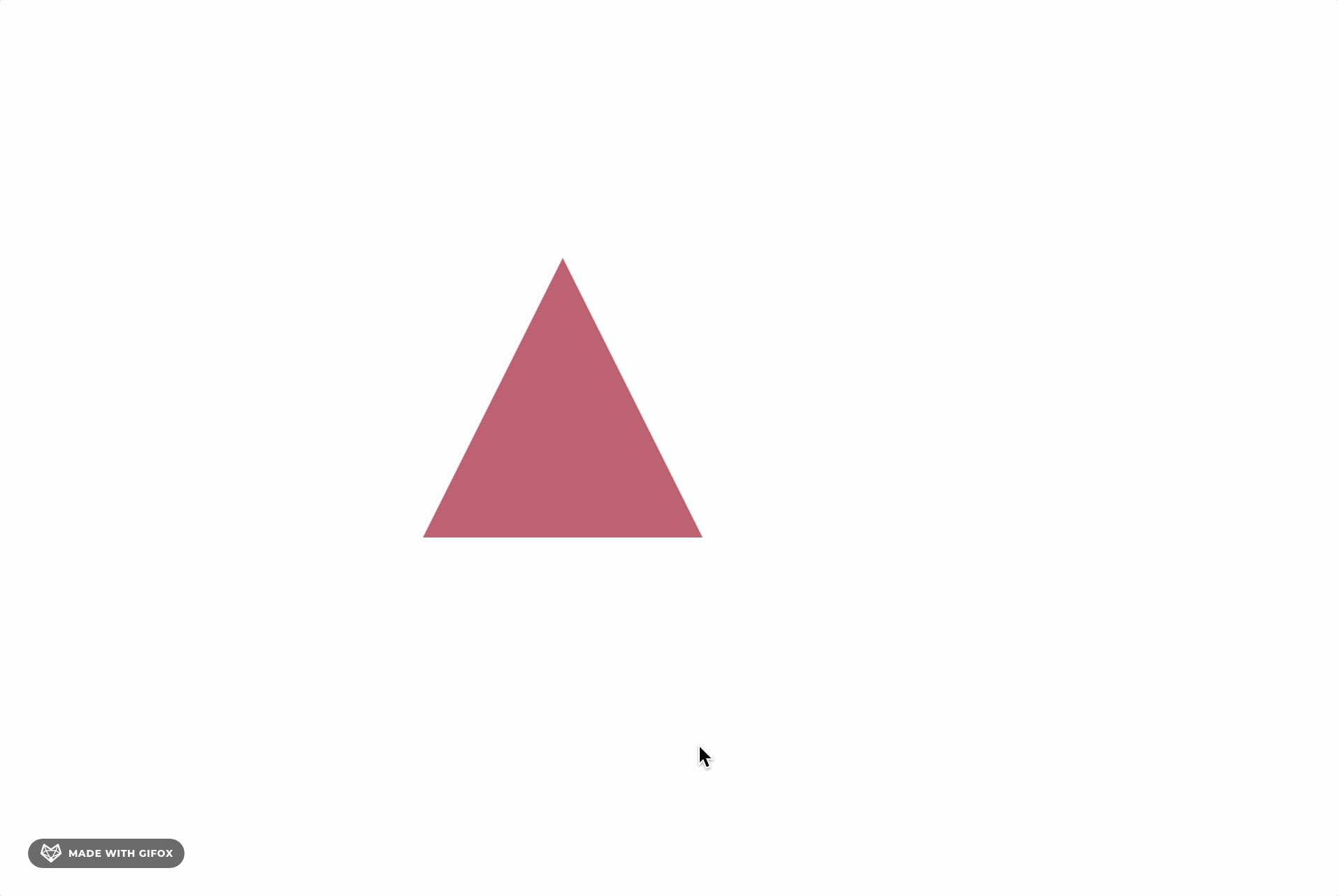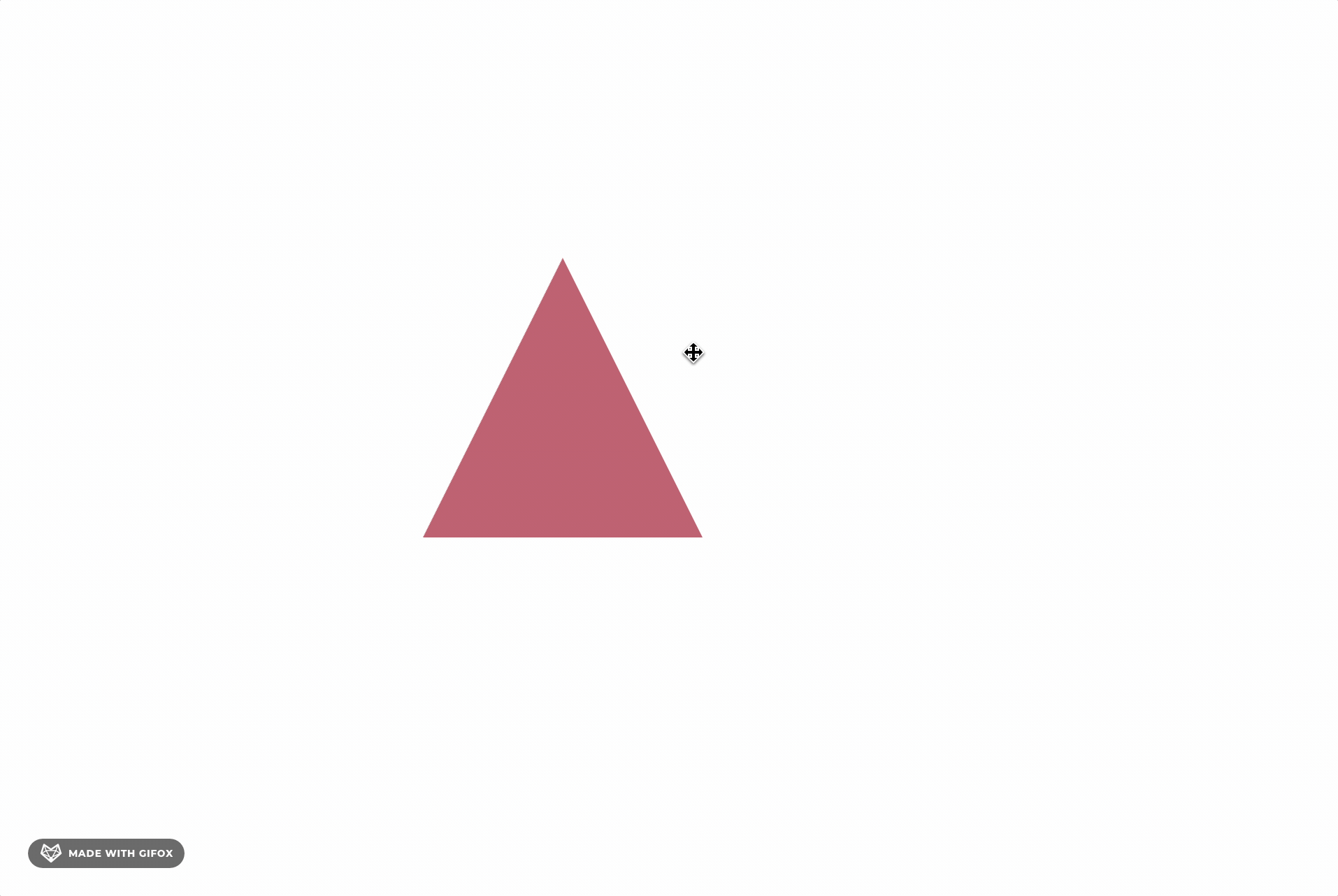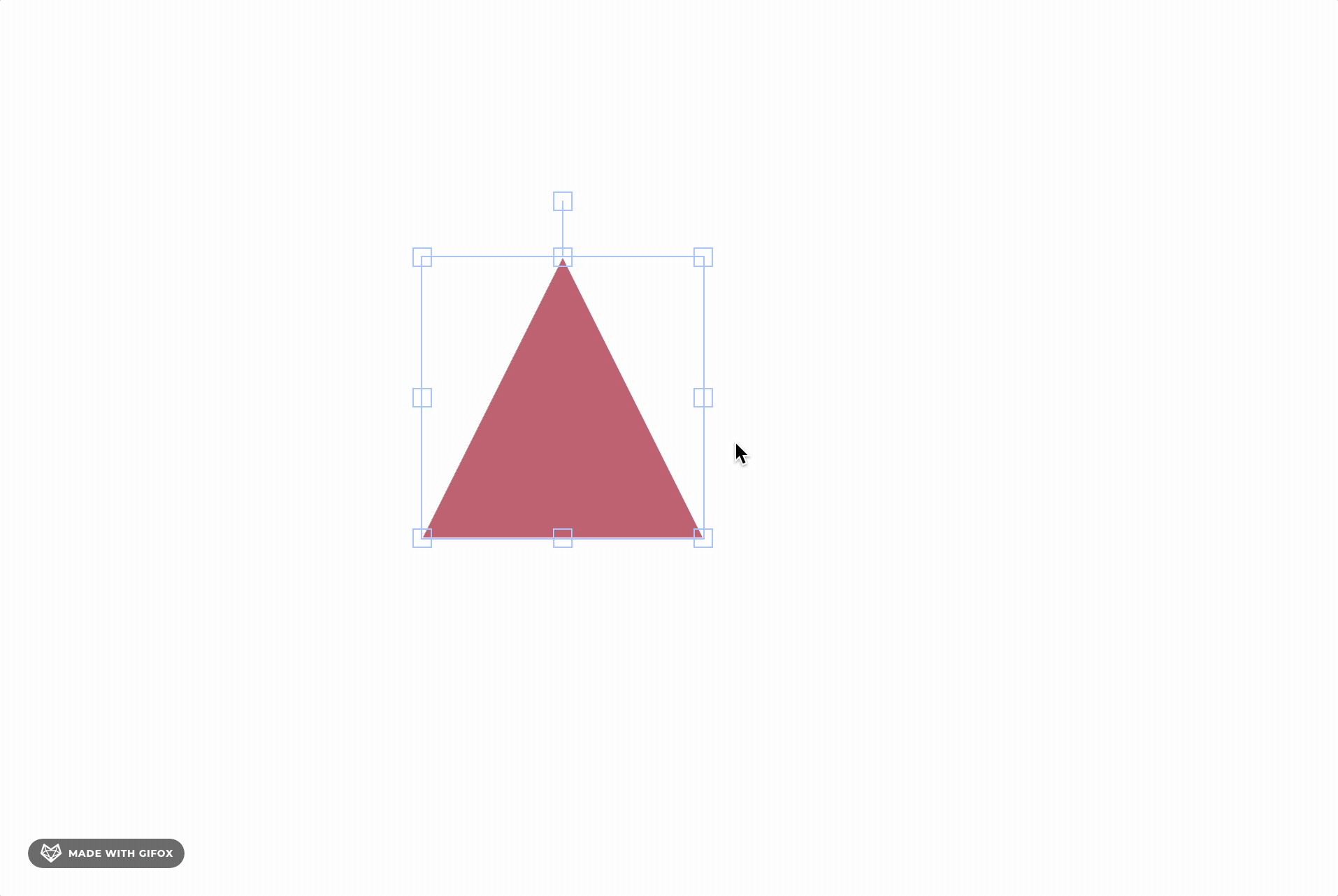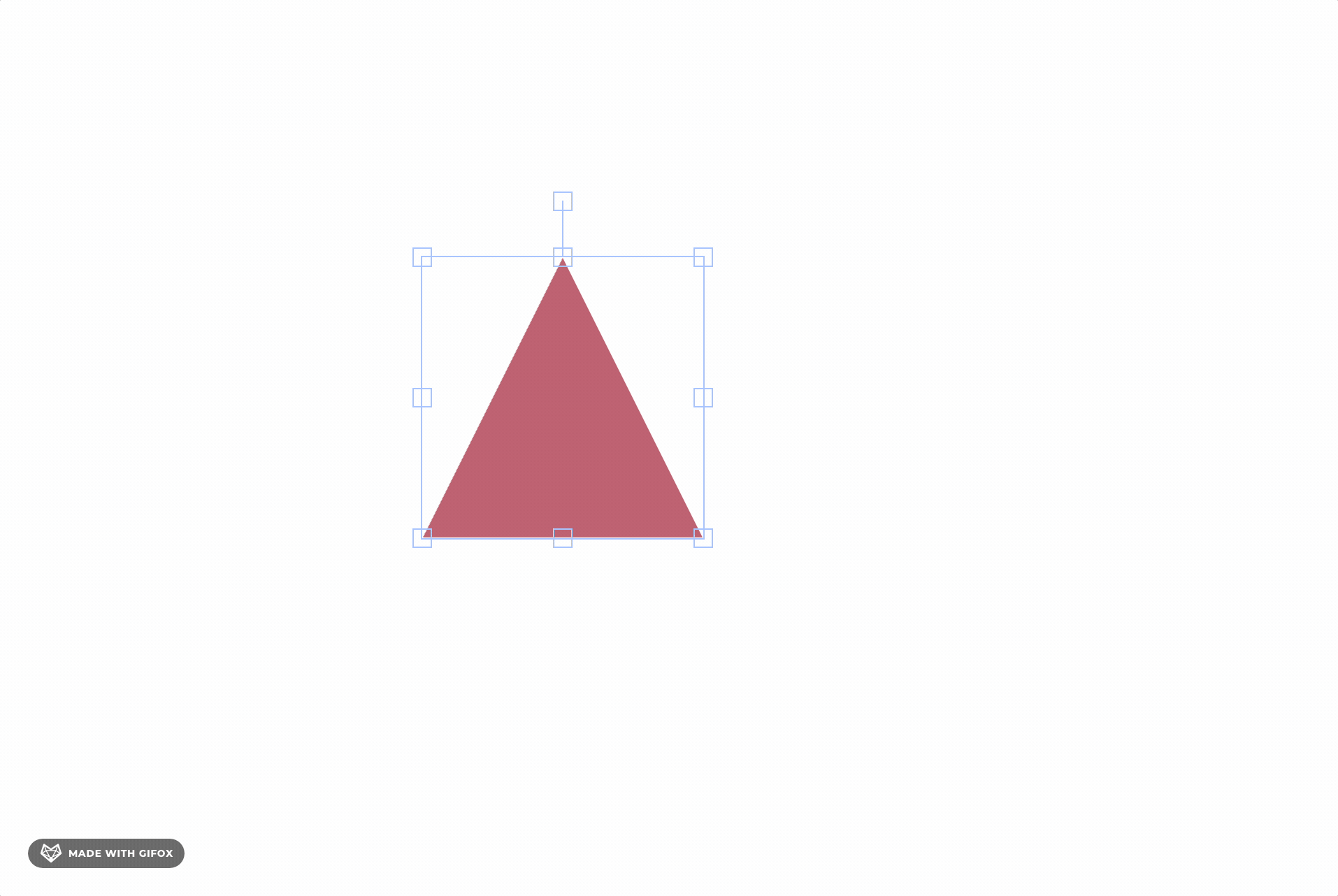
我们不难发现,在 Fabric.js 中也是通过 AABB 包围盒进行点选物体的。
演示地址: https://enson0131.github.io/mini-fabric-whiteboard/
点射法
对于矩形,我们可以很方便地计算出点是否在矩形内,在不借助包围盒的情况下,是否可以判断点在多边形内呢?
显然是可以的,常见的算法是 点射法,这种方法的核心思想是通过从目标点 P(x,y) 向任意方向发射一条射线,通常选择水平或垂直方向以简化计算,然后统计射线与几何区域的边或面相交的次数。
如果射线与边/面的交点数是奇数,点在多边形内部。
如果交点数是偶数,点在多边形外部。
大致可以在脑海里想象下👇
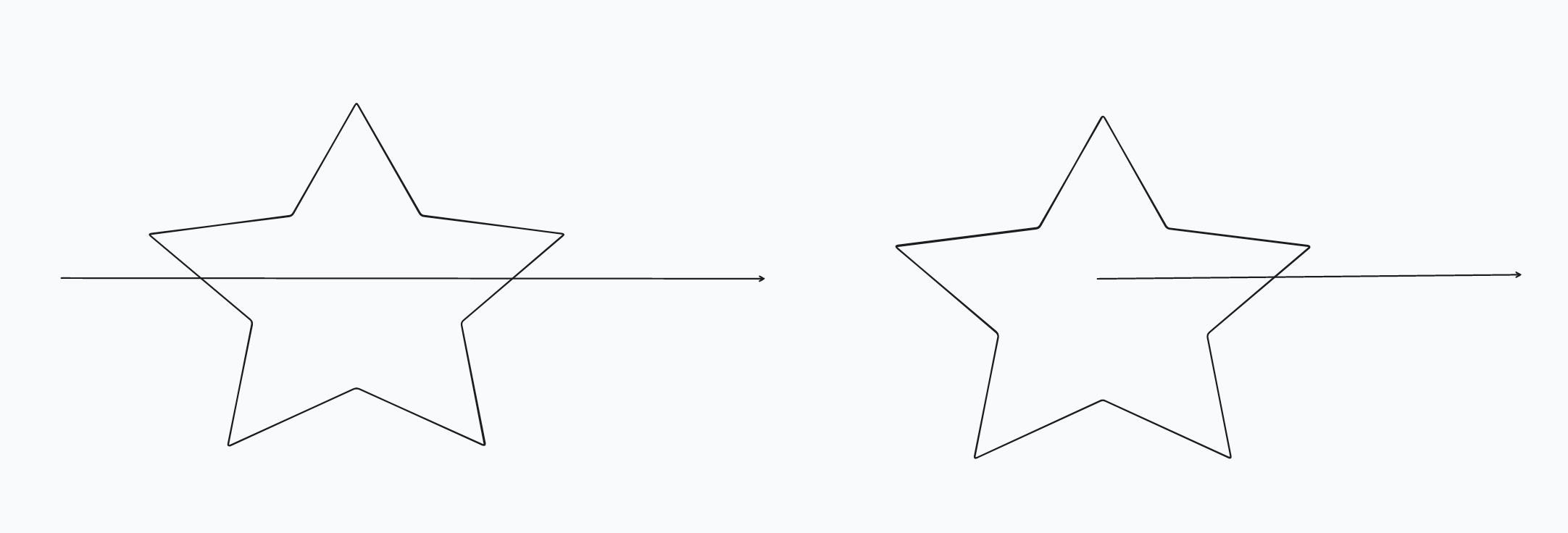
应该有不少同学已经想象到一些边界场景:
点在多边形的顶点上
点所在的射线穿过图形的顶点上
点的射线穿过图形的一条边
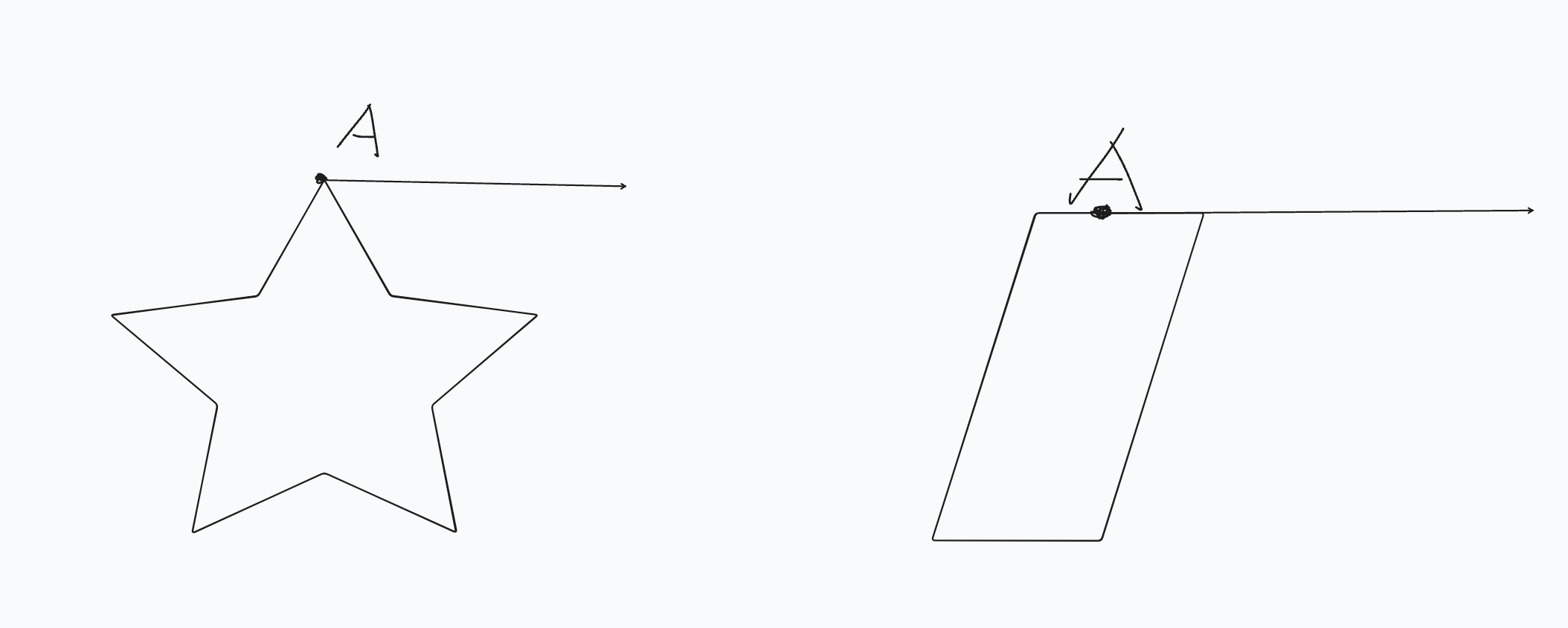
基于第一种场景,可以通过业务场景决定是否在多边形内/外。
基于第二种场景,常见的会将其判断为一个交点,而第三种场景则可以简单判断为无交点。
通过 点射法,我们可以将问题转化为射线与多边形各个边的交点,也就是简化成了求解一元线性方程组。
数学原理:
射线方程:`y = b1x + a1`
边界线段方程:`y = b2x + a2`
交点处:`b1x + a1 = b2x + a2`
求解x坐标:x = `-(a1 - a2)/(b1 - b2)`。
下面是一些伪代码:
b1 = 0; // b1 / b2 是斜率
b2 = (iLine.d.y - iLine.o.y) / (iLine.d.x - iLine.o.x); // iLine.d 多边形线段的终点、iLine.o 是多边形线段的起点
a1 = ey - b1 * ex;
a2 = iLine.o.y - b2 * iLine.o.x;
xi = -(a1 - a2) / (b1 - b2); // 求俩个直接的交点,即求出交点的 x 坐标 即 xi = a1 - a2 / b2;b1 = 0; // b1 / b2 是斜率
b2 = (iLine.d.y - iLine.o.y) / (iLine.d.x - iLine.o.x); // iLine.d 多边形线段的终点、iLine.o 是多边形线段的起点
a1 = ey - b1 * ex;
a2 = iLine.o.y - b2 * iLine.o.x;
xi = -(a1 - a2) / (b1 - b2); // 求俩个直接的交点,即求出交点的 x 坐标 即 xi = a1 - a2 / b2;点在多边形内的其他方法
用 canvas 自身的 api isPointInPath 传送门 👉: https://developer.mozilla.org/zh-CN/docs/Web/API/CanvasRenderingContext2D/isPointInPath
将多边形切割成多个三角形,然后判断点是否在某个三角形内部
转角累加法(点连接各个顶点,计算夹角是否等于 360)
面积法 (点连接各个顶点形成三角形,计算面积是否等于图形的面积等)
优化
优化1: 记录最近的这个物体,下次再次判断这个物体
细心的同学不难发现,鼠标在移动的时候,我们都需要判断是否点是否在物体上,开销比较大,常见可以使用 节流 的方式进行优化。
当然,还有另一种方式就是记录最近的这个物体,下次优先再次判断这个物体,因为我们会觉得选中过的物体,再次选中的概率会很大
优化2: 判断是否是透明区域
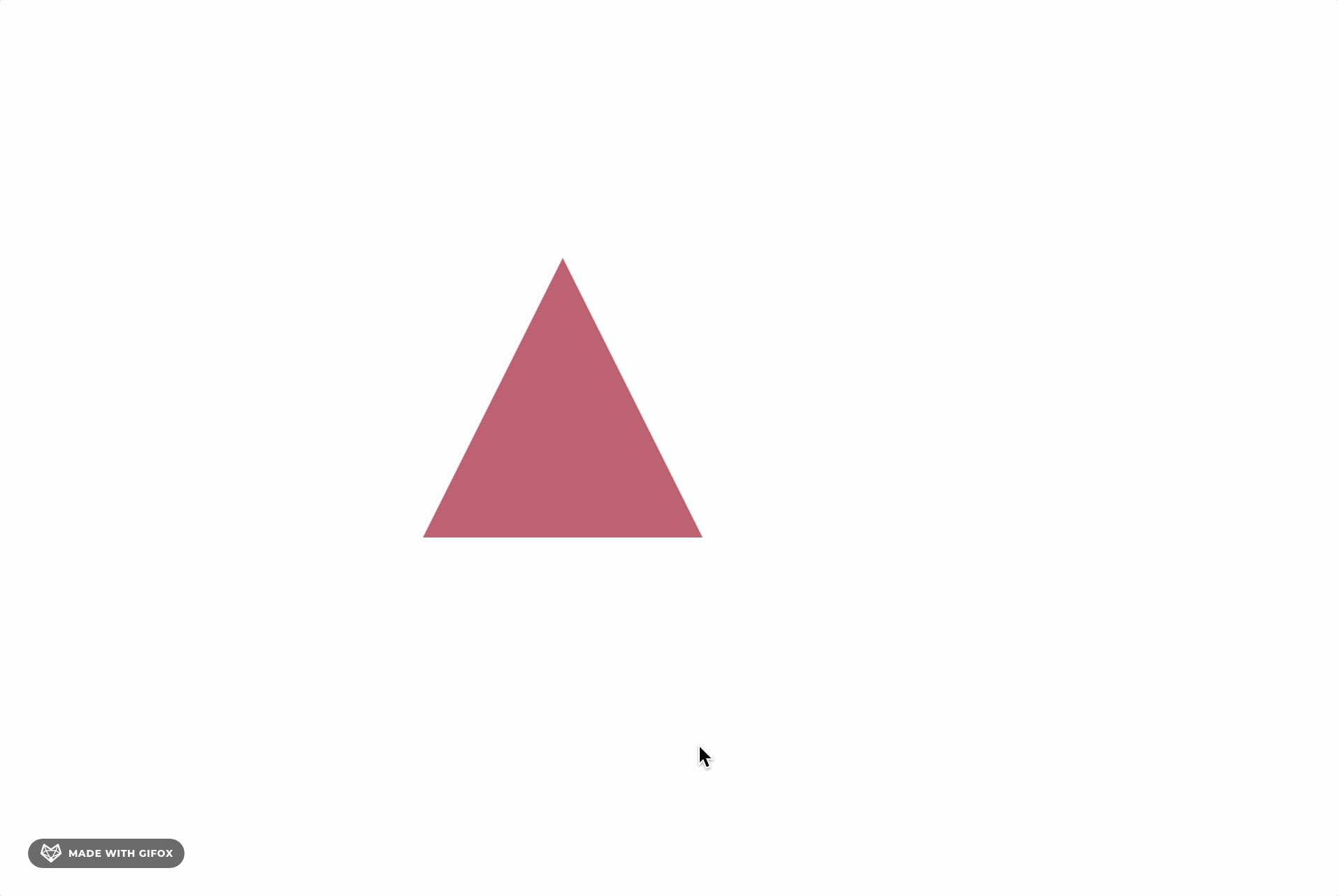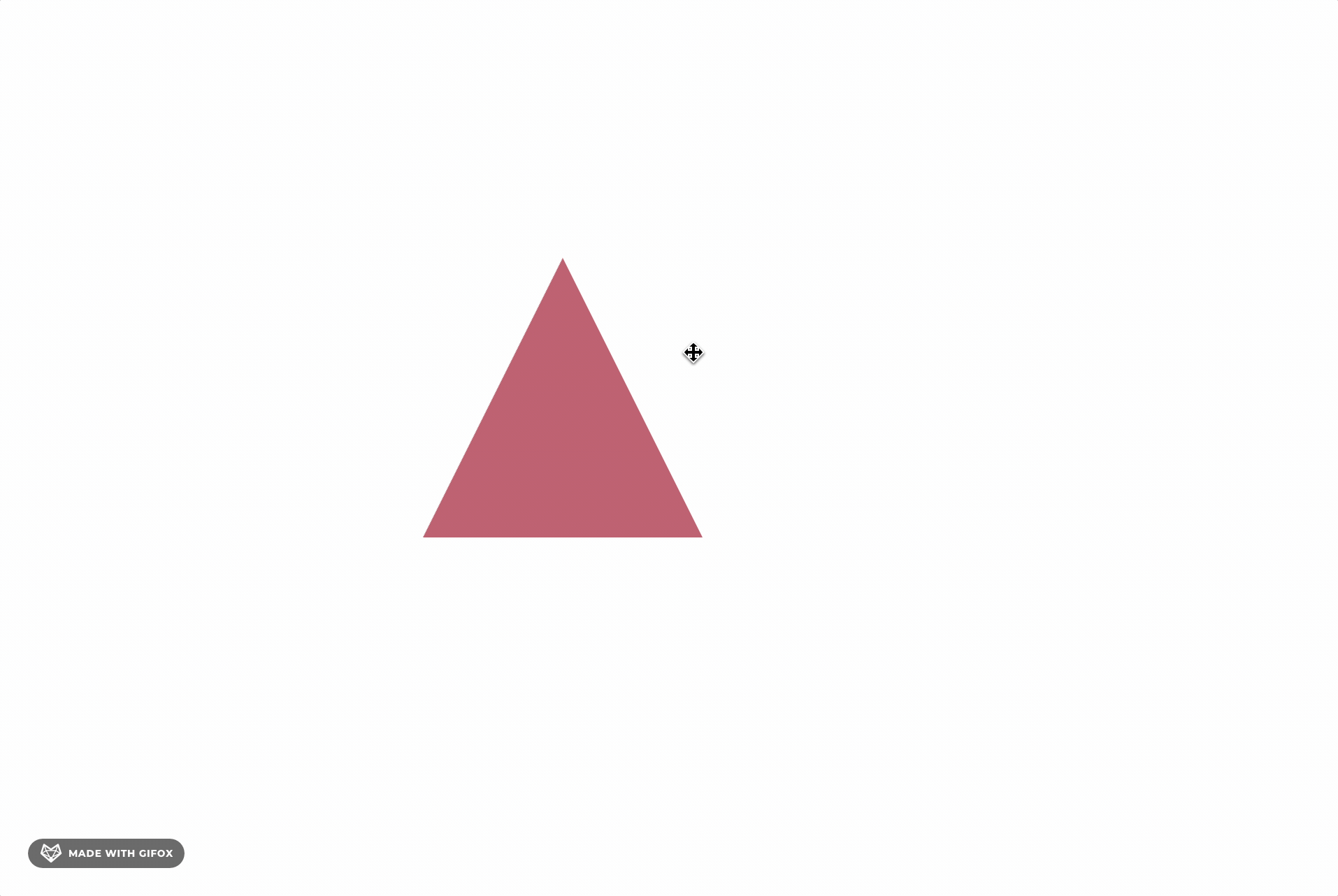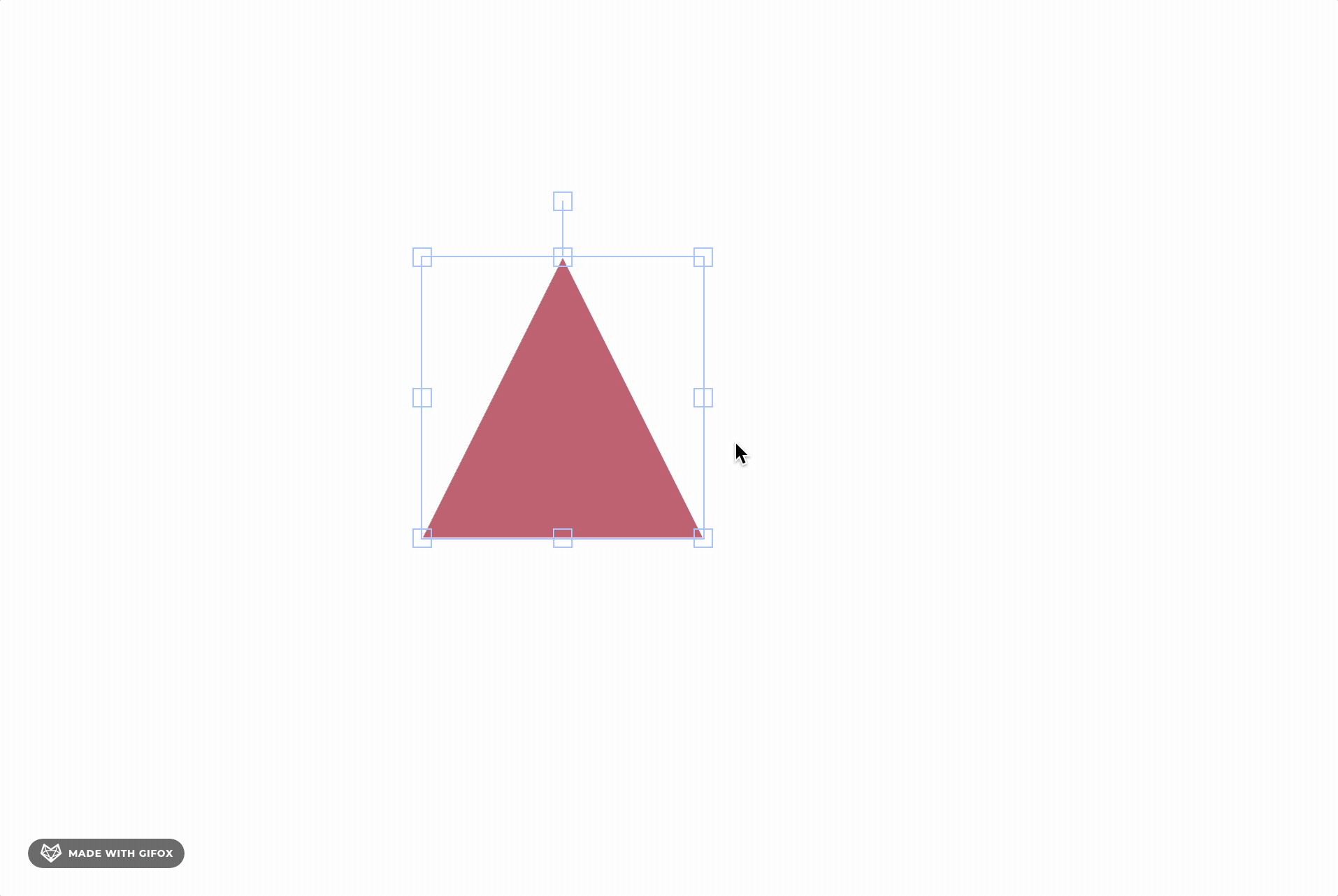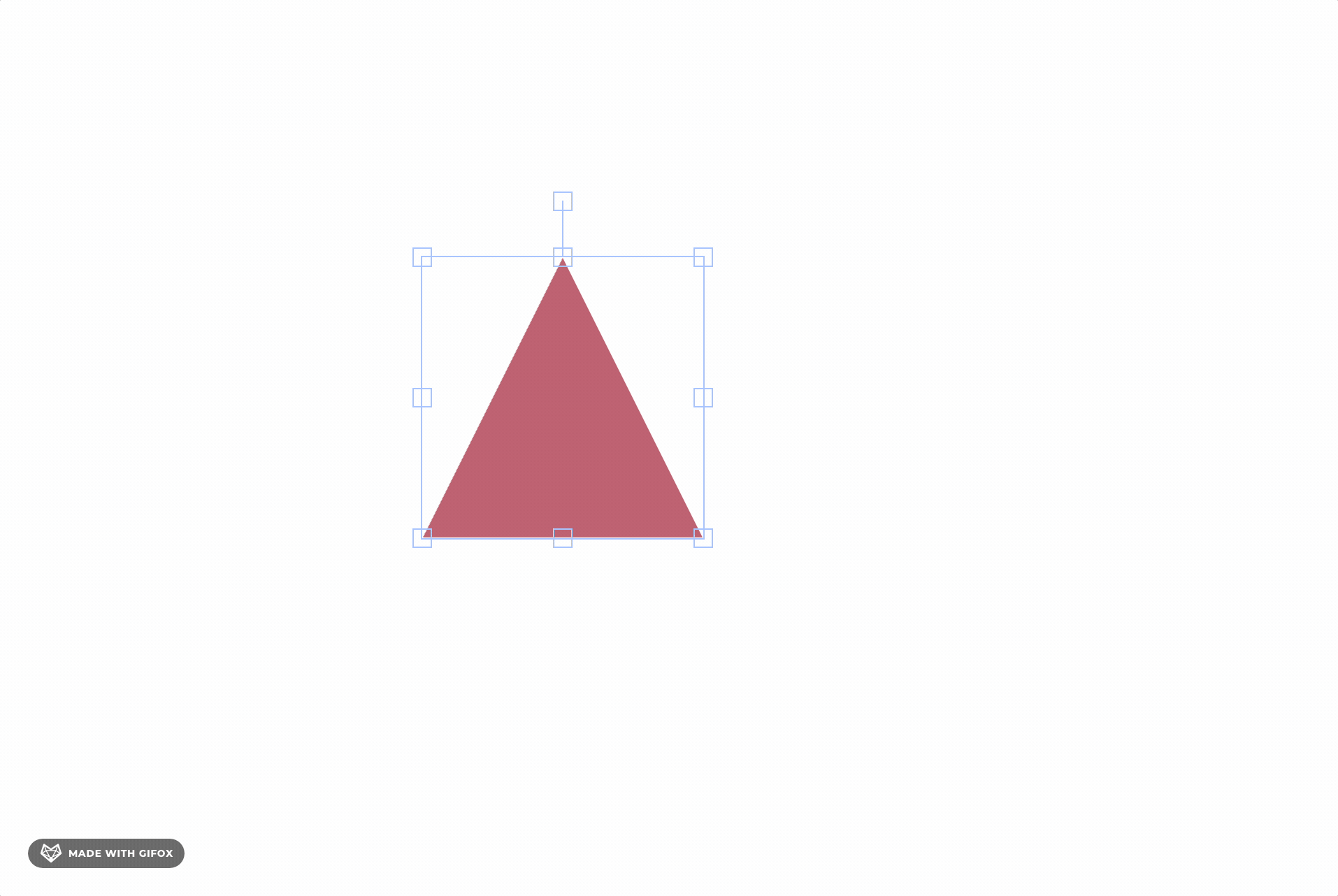
如上图,我们发现,当我们鼠标命中包围盒时,并非完全命中物体,常见可以通过判断透明区域,是否命中物体。
例如当我们判断命中包围盒时,在通过当前坐标点获取周围的像素,例如通过 ctx.getImageData可以获取当前 ctx Canvas 图层的图像数据,再进而判断是否都是透明度为 0 的像素。如果是则为空白区域、否则命中🎯。
let isTransparent = false; // 判断是透明度
const imageData = ctx.getImageData(x, y, width, height);
for (let i = 3; i < imageData.data.length; i += 4) { // 只要看第四项透明度即可
let temp = imageData.data[i];
isTransparent = temp <= 0;
if (isTransparent === false) break; // 找到一个颜色就停止
}let isTransparent = false; // 判断是透明度
const imageData = ctx.getImageData(x, y, width, height);
for (let i = 3; i < imageData.data.length; i += 4) { // 只要看第四项透明度即可
let temp = imageData.data[i];
isTransparent = temp <= 0;
if (isTransparent === false) break; // 找到一个颜色就停止
}